Many of the nearly 300 underground waste storage tanks throughout the DOE complex—more than half of them at Washington’s Hanford Site—contain complex mixes of radioactive and chemical products. Under a variety of chemical and physical conditions, bubbles of gas are trapped in the waste, at least temporarily, by capillary forces and the strength of the surrounding material. Because retained bubbles are compressible, the surface levels in some tanks respond to the constant fluctuations in barometric pressure. Drops in barometric pressure induce apparent increases in waste volume when the bubbles expand. Rising barometric pressure depresses the surface of the waste as the bubbles are compressed. Variations in the size and shape of the bubbles can influence whether, when, and how fast they rise to the surface. These would be interesting but insignificant phenomena if the bubbles were innocuous, but they are typically a flammable mixture of hydrogen, ammonia, and nitrous oxide. There is potential for these gases to burn if a large and rapid release coincides with an ignition source. Consequently, whether the bubbles remain trapped in the waste or rise to the surface, they pose safety problems for both continued safe storage and retrieval and treatment processes. Reliable knowledge of the volume of retained gas is essential to establishing and managing the safety hazard of the tanks. Mathematical models based on sound theories are needed to calculate retained gas volume from interrelated patterns of measured waste levels and barometric pressure changes. Such estimates are highly desirable because direct, in situ measurements are very expensive in any tank and impossible in many. Combining disciplines Specific goals were to
Because bubbles retained in slurries and sludges behave differently, the research combines expertise of team members from several disciplines. William Rossen, of the University of Texas at Austin, is modeling bubble behavior in particulate materials (slurries). Modeling studies on sludges are being conducted from the viewpoints of both solid mechanics (by Guillermo Terrones at PNNL) and fluid mechanics (by Morton Denn and Susan Muller at Lawrence Berkeley National Laboratory). Gauglitz is supervising experimental studies at PNNL on both slurries and sludges. Lab experiments shed light on bubble
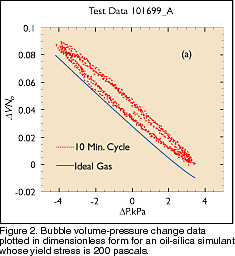
behavior Experiments have been performed on both water- and oil-based simulants, but each has limitations. Figure 2 shows normalized pressure and level data from a single-bubble experiment. The data shows “hysteresis,” where the level depends on the pressure history in addition to the current pressure, indicating that some stresses must be overcome before bubble volume responds.
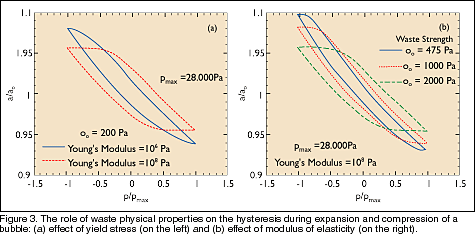
The current model is significantly more rigorous than those of previous studies at PNNL and has yielded significant new results. New estimates of material strength based on the model are an order of magnitude smaller than previous calculations, which accounted poorly for elastic and plastic regions and residual stresses. Figure 3a shows that increasing the waste strength causes an increasing hysteresis in the relationship between bubble radius and pressure. This occurs because the waste, which is a soft solid, resists the expansion and compression of the bubble. Figure 3b shows that the hysteresis also depends on Young’s modulus (the ratio of a simple tension stress applied to a material to the resulting strain parallel to the tension).
This model enables the engineer to estimate the rate at which bubbles rise through the sludge as a function of the specific barometric pressure history. Within the model assumptions, bubbles rise as long as the magnitude of the pressure fluctuations (regardless of whether the medium is compressed or decompressed) exceeds the yield condition for the material. Work continues to gain a better understanding of the interplay among the various parameters and the feasibility of estimating mechanical properties. Fluid mechanics modeling They discovered limitations in commercially available fluid mechanics modeling codes when applied to this study and developed a more valid finite-element code. The code has been validated in pipe flow and squeeze flow. Work continues to refine the code and reduce error in the model. Slurry modeling The compressibility of the gas is a function of its pressure, which is the sum of barometric pressure, the known hydrostatic pressure from the liquid in the tank, and capillary pressure in the porous medium formed by the slurry. Three time scales are involved. Over a period of months or years, chemical reactions in stored liquid waste create volatile components that diffuse to and accumulate in bubbles. Bubble mass and volume increase slowly at fixed liquid pressure, determining the initial states of bubbles when barometric pressure changes. On a time scale of hours, bubble volume responds to changes in barometric pressure. On this time scale, effective compressibility is observed. On a still shorter time scale, seconds or less, interfaces between bubbles and the viscous liquid advance or retreat impulsively, driven by capillary forces. For expanding bubbles, whether due to accumulation of mass over a period of months or to a short-term decrease in barometric pressure, impulsive jumps occur from the throat of one pore to near the throat of the next. During pressure increases, however, interfaces jump from pore body to pore body. Because most jumps in tank waste have occurred during the slow growth of bubbles over months, most bubbles are lodged at pore throats, ready to jump again if pressure decreases. However, these same bubbles do not jump backwards if pressure increases, until their interfaces first retreat to pore bodies. Thus, a population of bubbles has a significantly higher effective compressibility during decreasing rather than increasing pressure. The project’s constricted-tube model can fit tank data with level-pressure hysteresis, but ambiguity remains on the relationship between bubble geometry and capillary pressure. The PNNL experiments or other threads of the project may provide the information needed to solve that problem. For more information on this research, contact lead principal investigator Phil
Gauglitz, PNNL, (509) 372-1210, phillip.gauglitz@pnl.gov. |
 Through the
Through the 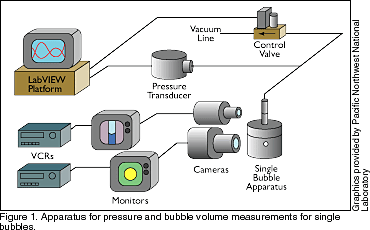
 Solid
mechanics modeling
Solid
mechanics modeling